문제

#98. Validate Binary Search Tree

Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1.

Input: root = [2,1,3]
Output: true

Example 2.

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints.

The number of nodes in the tree is in the range [1, 104].
-2^31 <= Node.val <= 2^31 - 1

해법

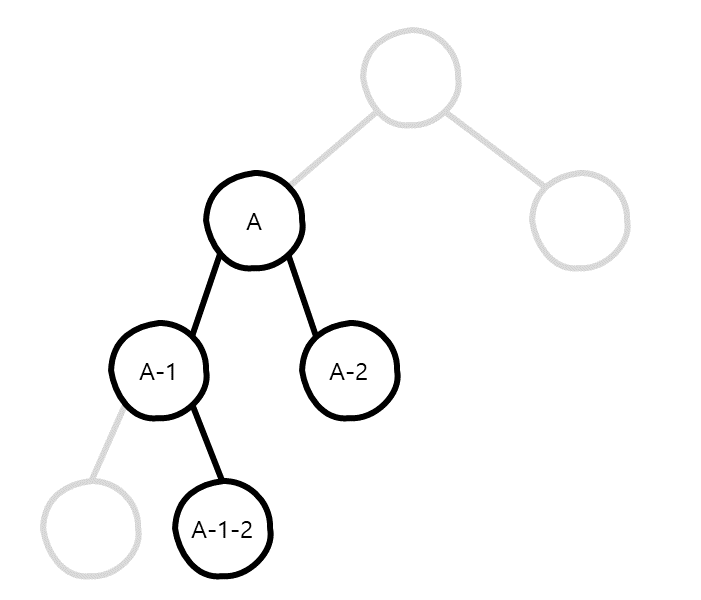
특정 노드 (A)를 기준으로 왼쪽 자식노드 (A-1)는 부모노드 (A)보다 값이 작아야 하며, 오른쪽 자식노드 (A-2)는 부모노드 (A)보다 값이 커야 합니다.
뿐만 아니라, 왼쪽 자식노드 (A-1)의 오른쪽 자식노드 (A-1-2)는 부모노드 (A-1)보다는 커야하며, 조상노드 (A)보다는 작아야 하는 조건을 만족해야 한다는 부분이 중요합니다.

나의 해법 (Recursion)

성능

• 시간 복잡도 : O(n)
• 공간 복잡도 : O(n)

해법

재귀 호출을 통한 후위 순회(Postorder)를 이용한 해법으로, root 노드로부터 시작하여 노드의 값이 유효한지 체크하고, 유효하다면 재귀 호출을 통해 자식노드를 확인한다.

1. root 노드부터 isValidBST() 함수를 호출한다.
   최소 한계값 및 최대 한계값은 없으므로 null을 입력한다.
2. isValidBST() 함수 내에서 입력받은 node의 값이 null이면 true를 반환한다.
3. 최소 한계값인 minLimit이 존재한다면, node의 값이 최소 한계값보다 작거나 같다면 false를 반환한다.
4. 최대 한계값인 maxLimit이 존재한다면, node의 값이 최대 한계값보다 크거나 같다면 false를 반환한다.
5. 왼쪽 자식노드가 유효한지 확인한다.

5-1. isValidBST() 함수를 재귀 호출하며, 인자로 왼쪽 자식노드 node.left, 최소 한계값 minLimit 그리고 최대 한계값으로 현재 노드의 값 node.val을 전달한다.
(왼쪽 자식노드는 부모 노드보다 작아야 하기 때문에 최대 한계값으로 현재 노드의 값을 전달한다.)
5-2. 왼쪽 자식노드가 유효하지 않다면 false를 반환한다. 6. 오른쪽 자식노드가 유효한지 확인한다.
6-1. isValidBST() 함수를 재귀 호출하며, 인자로 오른쪽 자식노드 node.right, 최소 한계값으로 현재 노드의 값 node.val 그리고 최대 한계값 maxLimit을 전달한다.
(오른쪽 자식노드는 부모 노드보다 커야 하기 때문에 최소 한계값으로 현재 노드의 값을 전달한다.)
6-2. 오른쪽 자식노드가 유효하지 않다면 false를 반환한다. 7. 최종적으로 모든 노드가 유효하다면 true를 반환한다.

Java 코드

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class ValidateBinarySearchTree {

  public boolean isValidBST(TreeNode root) {
    return isValidBST(root, null, null);
  }

  public boolean isValidBST(TreeNode node, Integer minLimit, Integer maxLimit) {
    if (node == null) return true;

    if (minLimit != null && node.val <= minLimit) return false;
    if (maxLimit != null && node.val >= maxLimit) return false;

    if (!isValidBST(node.left, minLimit, node.val)) return false;
    if (!isValidBST(node.right, node.val, maxLimit)) return false;

    return true;
  }

}

나의 해법 (Iteration)

성능

• 시간 복잡도 : O(n)
• 공간 복잡도 : O(n)

해법

Stack을 사용하여 재귀 호출 대신 반복문을 통한 중위 순회(Inorder)를 이용한 해법이다.

1. 현재 노드 node에 루트 노드 root를 할당한다.
2. 스텍 nodeStack에 값이 존재하거나, 현재 노드 node가 존재하는 동안 반복한다.

2-1. 현재 노드 node가 존재하는 동안 반복한다.
2-1-1. nodeStack에 node를 담는다.
2-1-2. node에 왼쪽 자식노드 node.left를 할당한다.
2-2. nodeStack에서 노드를 하나 빼서 node에 할당한다.
2-3. untilMinVal에 값이 존재하면, 현재 노드의 값 node.val과 비교하여 유효하지 않을 경우 false를 반환한다.
(중위 순회를 통해 진행하므로, 조회되는 노드의 값은 오름차순으로 조회되어야 유효하다.)
2-4. untilMinVal에 현재 노드의 값 node.val을 할당한다.
2-5. node에 오른쪽 자식노드 node.right를 할당한다.
3. 모든 순회가 끝나면 true를 반환한다.

Java 코드

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class ValidateBinarySearchTree {

  public boolean isValidBST(TreeNode root) {
    Stack<TreeNode> nodeStack = new Stack<>();

    Integer untilMinVal = null;
    TreeNode node = root;
    while(!nodeStack.isEmpty() || node != null) {
      while(node != null) {
        nodeStack.push(node);
        node = node.left;
      }

      node = nodeStack.pop();
      if (untilMinVal != null && untilMinVal >= node.val) return false;
      untilMinVal = node.val;

      node = node.right;
    }

    return true;
  }

}

코멘트

여기서의 핵심은, 특정 노드의 유효성을 확인할 때 부모노드 하고만 비교하는 것이 아니라, 조상 노드도 고려해야 한다는 것 입니다.